genetic-selectR Package Development

I Introduction

In this project, we created an R package implementing genetic algorithms that efficiently selects the most optimized combination of covariates from multidimensional datasets for generalized linear modeling. We allow users to choose their own fitness functions and several different genetic operators, such as crossover and mutation. We also tested all of our functions using different datasets and criteria. Further details of the package are shown below.

All code for this project can be found in this GitHub repository.

II Algorithms

In order to implement this genetic selection algorithm, we partitioned each step into separate helper functions and formatted our main select function such that it carries out the genetic algorithm by calling each of the helper functions. Because each of our helper functions has a well-defined task, this also allowed each of us to focus on building functions without having to consult each other about any minute changes that were being made. Each helper function is briefly described as follows:

Calculate Fitness and Find the Best Model

We will first discuss the calc_fit function, where we obtain the fitness values of each gene in the population. The user can specify their own fitness function and regression type, which have default values AIC and linear regression, respectively. We then call the find_best_model function to determine which gene has the best fitness score in the current generation.

Select Parents

Next, we will go over the select_parents function, where we specify which genes in the current population will become parents of the next generation. This decision is made based on their fitness scores. We offer two selection methods in this function: prop_rand and tournament. The prop_rand method chooses one parent with probabilities proportional to the fitness functions and chooses the other parent at random. The tournament method divides the population into different sections and picks the best gene in each section to be a parent.

Crossover

In the crossover_p_split function, we crossover each pair of parents chosen by the previous helper function to create a new generation of offspring. We allow users to choose the number of split points and we divide both parents into (p+1) parts. Then, for each section of the divided genes, we randomly determine which parent’s gene a new offspring will be inheriting. The parent’s piece that was not chosen will be inherited by the other offspring, thereby creating two offspring from each pair of parents.

Mutation

Next, themutate_genes function decides whether genes will mutate or not. Each gene has an independent probability of mutating. While the mutation rate has a default value of 0.01, we also allow users to manually choose the rate. If chosen, a new allele is then chosen completely at random from the genetic alphabet. In our case, we are only considering binary genes so the entirety of our genetic alphabet is comprised of zeros and ones, meaning there is a 50% chance that the new allele chosen will be the same allele that the gene already possessed.

Select

We will now be discussing our main select function which calls upon all of the previously mentioned functions. We first call the gen_firstgen function to randomly generate the first generation of genes. We then call upon the functions explained above in order. The max_iter argument specifies how many generations our algorithm will go through before stopping. It has a default value of 50 but can also be determined by users. In order to evaluate the diversity among each population of genes, we observe the scaled relative error between the best fitness score in our current generation and the best fitness score of our previous generation. If this relative error is less than the specified diversity threshold for three consecutive generations, we consider our algorithm to be convergence, end the selection process, and return our findings to the user. When designing the output of our select function, we decided to return the necessary information about the best model: the model itself, its fitness score, the generation it was created, and the average fitness score of that generation. Our function also prints a plot that visualizes the changes that occurred between the average and best fitness scores of the generations of genes created during the process and highlights the point at which the best model was created.

III Results

To put our algorithm into action, we utilized the “Boston” dataset from the MASS library because it is a linear dataset that is commonly used. We will now explore how different methods and parameters affect the algorithm’s rate of convergence.

Default Settings

In this section, we showcase our algorithm’s performance when using all the default methods and parameters. The result is shown below:

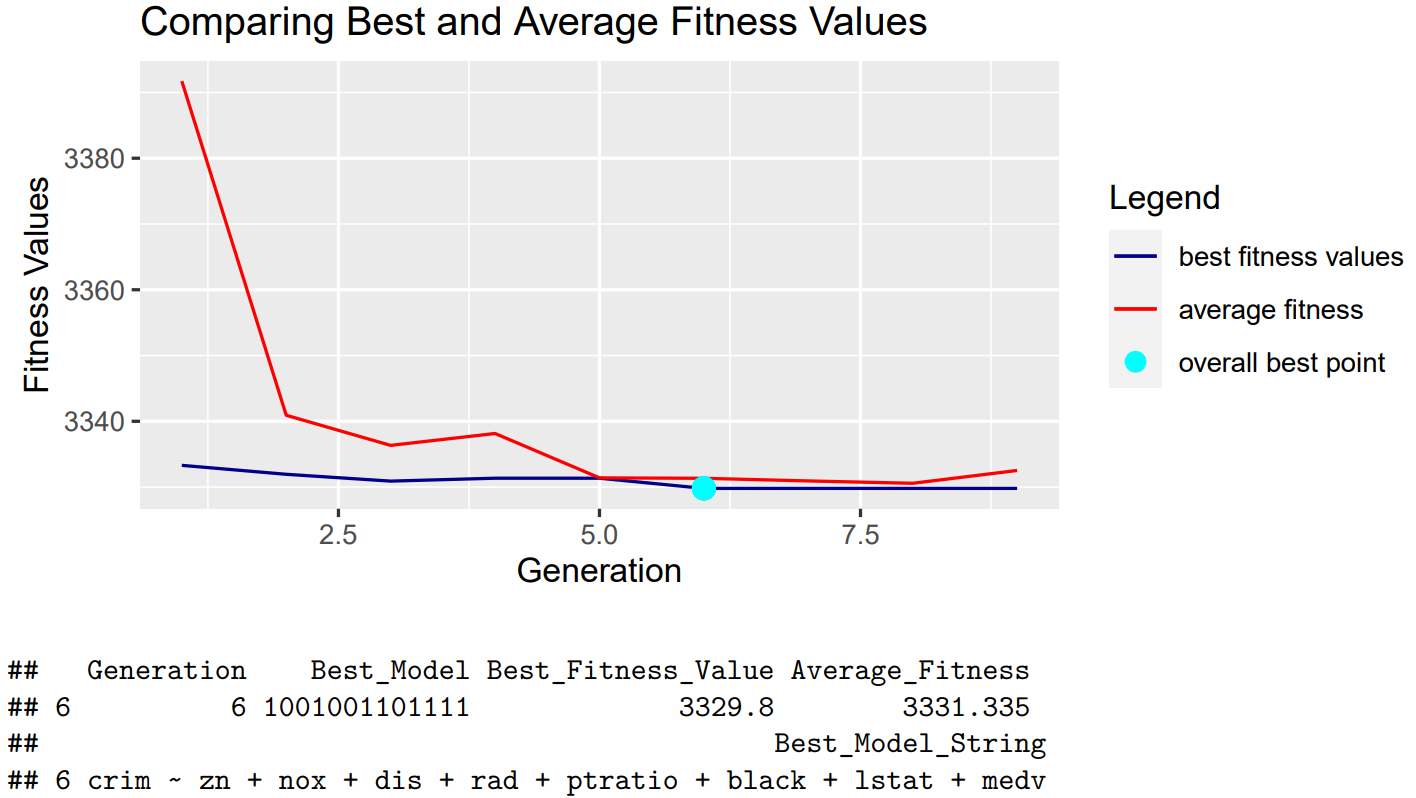
We can see that using the default methods with the Boston data set results in fast convergence. We also saw similar outcomes when using other variables, as most tests usually converged within ten generations. Therefore, we determined that our default values are set appropriately since we are able to obtain our best model efficiently under these settings.

Changing the Number of Partitions

Next, we increased our crossover points from default 1 to 6 and observe the changes that occur:

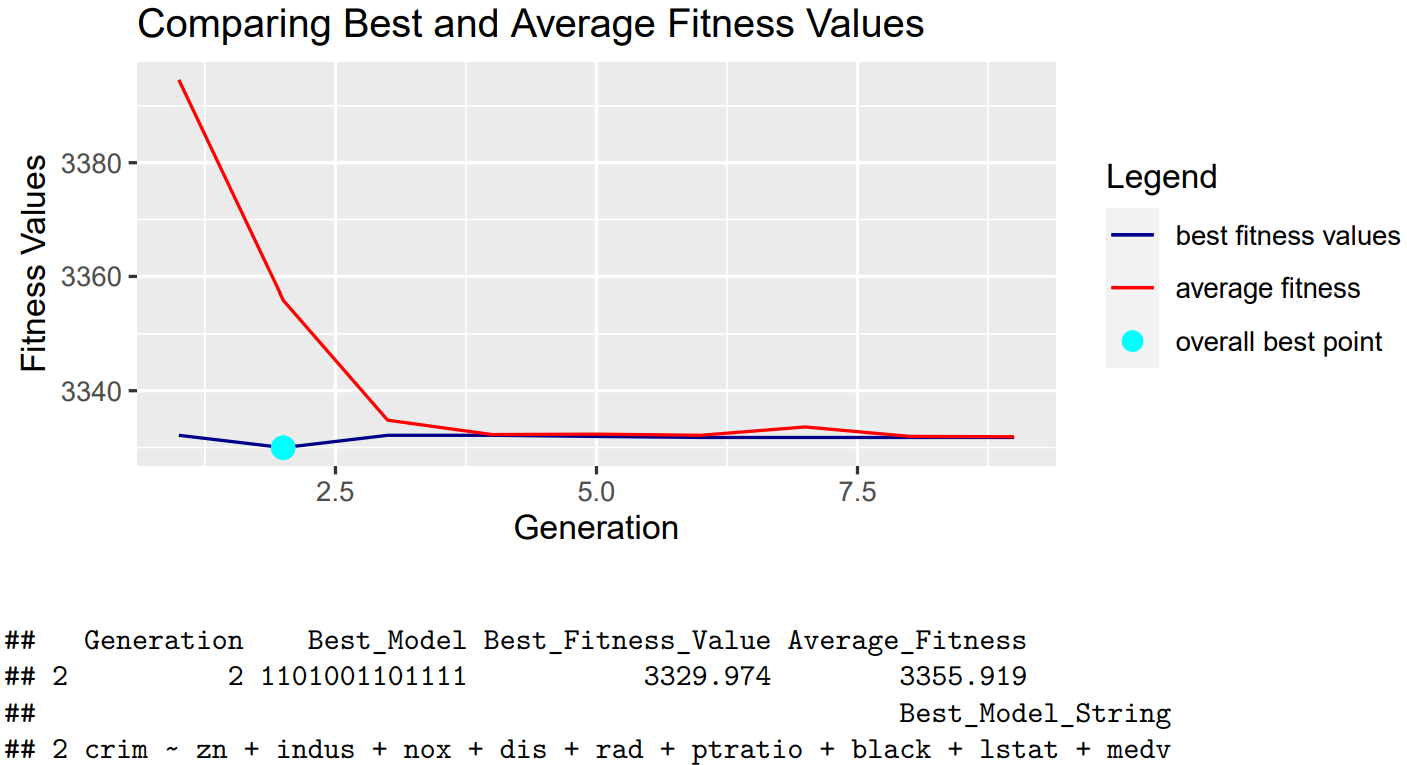
With these findings, we concluded that increasing the number of crossover points results in faster convergence.

Changing the Mutation Rate

We continued by changing our mutation from 0.01 to 0.1 to see how this would affect our results.

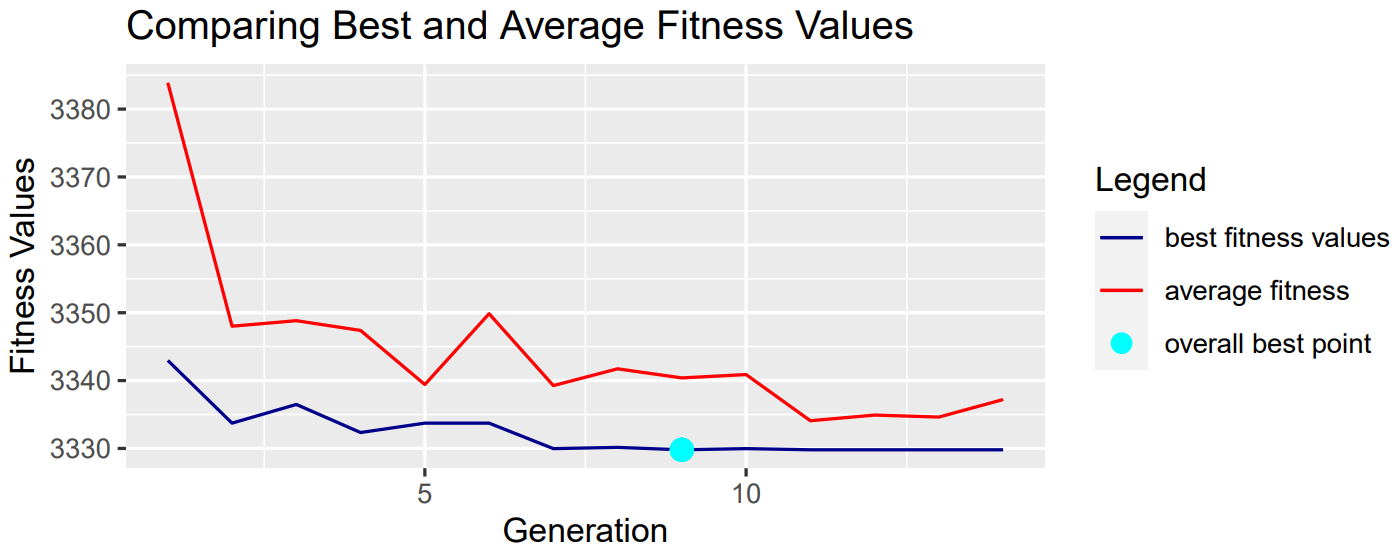
As expected, a smaller mutation rate generally leads to a better fit in each population overall. We can see above that a smaller mutation rate leads to faster convergence.

Changing the fitness function

We also explored the effects of altering our objective function to the log-likelihood option.

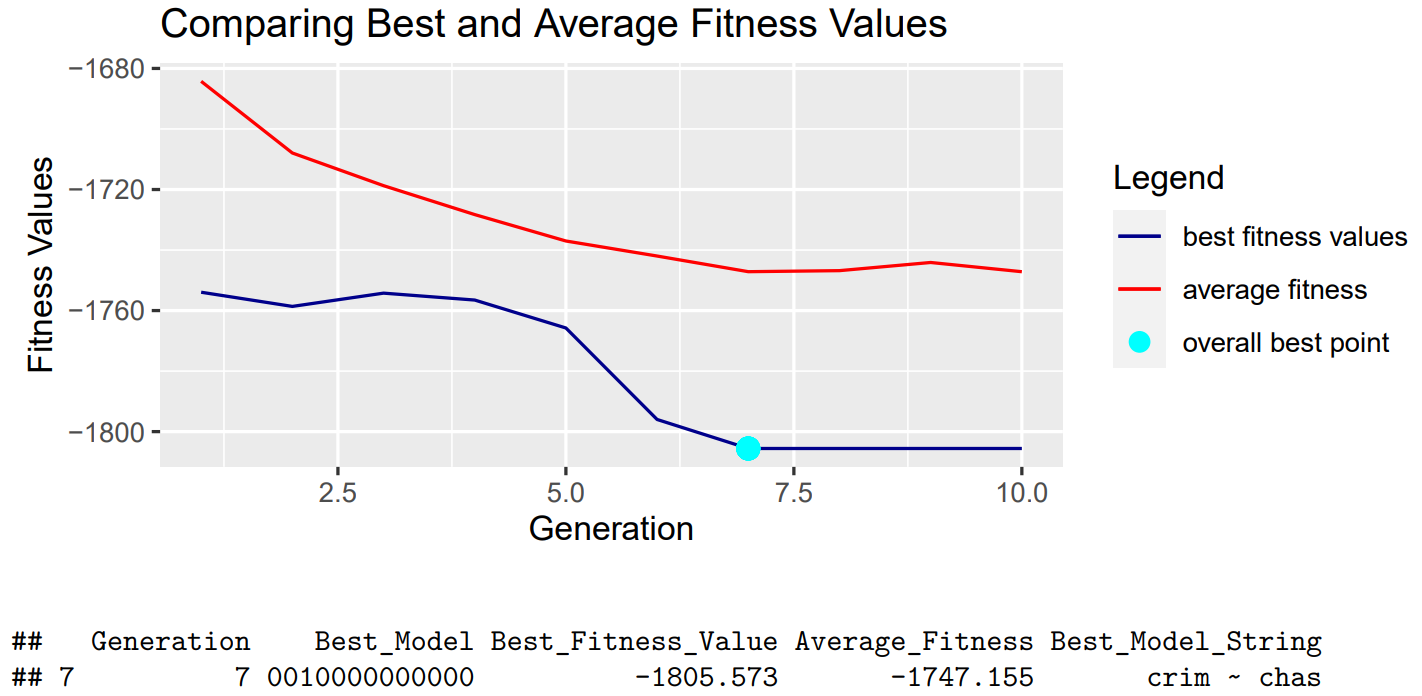
We can see we are able to reach convergence even when using different fitness functions, adding significant customization and flexibility to our package. This will allow users to implement our algorithm and cater to their specific needs.

IV Testing

The testing we carried out was focused on assessing whether our inputs and outputs were consistent with what we were expecting. We tested an extensive range of values in order to confirm that our functions would not break when dealing with inputs that were extreme, even if they were not practical. Naturally, we also ensured that our functions did not allow invalid inputs such as string values when it was expecting numeric values, and would return descriptive error messages when doing so. We confirmed that each helper function was returning an output that was consistent with the next helper function’s input as well. Additionally, we verified that none of our genes were being generated or modified to contain only zero alleles and ensured that if this were to happen, our simulate_gene function would be able to effectively resolve the problem.

VI Discussion

If users would like to implement our package in order to variable selection, we recommend experimenting with larger numbers of partitions for the crossover argument and smaller mutation rates. We would also suggest that users utilize the tournament method for the parent selection argument. Additionally, they should choose the fitness function and diversity threshold according to the specific regression problems they are considering.